In previous article, we discussed how to find the absolute value or modulus of a real number. To find out the modulus of a complex number in Python, we would use built-in abs() function. In addition to, we would calculate its modulus the traditional way.
But before that, a bit about complex number and its modulus.
A complex number consists of a real and imaginary part. Its of the form a+bi, where a and b are real numbers. Also, a is real part and bi is the imaginary part. We can calculate modulus of a complex number using Pythagoras theorem.
So, modulus of a complex number (x)-
![]()
Lets say we have,
x=a+bi
Therefore,
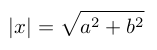
Modulus of a complex number in Python using abs() function
#Ask user to enter a complex number of form a+bj
x=complex(input("Enter complex number of form a+bj: "))
print("The modulus of ",x," is", abs(x))
We need to use complex data type to get the input from the user. It should of the form a+bj, where a and b are real numbers. For instance, 8+6j.
The complex number is stored in variable ‘x‘. Next, we used built-in abs() function to get the modulus of complex number.
For instance – 8+6j, we will get the result 10.
Modulus of a complex number in Python, the traditional way
Alternately, we can find out modulus of a complex number the traditional way.
#Ask user to enter a complex number of form a+bj
x=complex(input("Enter complex number in form a+bj: "))
import cmath
y=cmath.sqrt((x.real)**2+(x.imag)**2)
print("The modulus of ",x," is", y.real)
We would ask the user to enter a complex number of form a+bj and it gets stored in variable x. To perform mathematical functions on complex numbers, we would have to import cmath module.
Then, we would use x.real and x.imag to access real and imaginary parts of the complex number. ** is used for exponentiation. cmath.sqrt for finding out the square root and its result gets stored in variable y.
Lastly, we used print() function to display the desired outcome.
In conclusion, we have discussed how to get the modulus of a complex number in Python.





